Prime Factor Decomposition

Our paper today is dedicated to prime factor decomposition, a procedure that is basic and very important. This procedure is basic, and it is used to successfully implement many other mathematical procedures and operations that follow at a certain more difficult level!

In the text below you have the opportunity to see:

• Rules for prime factor decomposition.
• A few examples with branching of multiples.
• Table of prime factors of numbers from 1 to 100.
• Lots of video examples to help you gain skill and routine in practicing the factoring procedure.

Let’s start with:

Rules For Prime Factor Decomposition

Of course, before we start the procedure for prime factor decomposition, we need to define:

• A prime number is a number that can be divided only by the number 1 and by itself without getting a remainder!
• A complex number is a number which, in addition to being divisible by the number 1 and by itself, can be divided by at least one other part without obtaining a certain remainder!

Now that we already know what a prime number is and what a complex number is, we can start with the rule for dividing prime factors, which reads:

We divide a given number into multiples until all such multiples are in the form of prime multiples! This means that the arrangement and exact path of multipliers that we will choose during the procedure is not important at all.

Examples

Let’s look at some examples of prime factor decomposition, below in the same text!

Example 1: Break down the number 6 into prime factors!

We present the number 6 as a product of the numbers 2 and 3! Because the numbers 2 and 3 are prime numbers, the decomposition procedure ends immediately in the first step! Decomposing the number 6 into multiple branches looks like this:

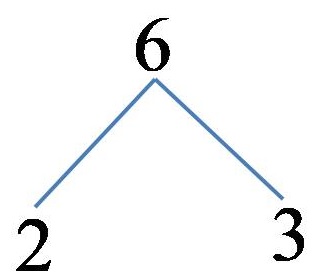
The number 6, through its prime multiples, can be represented as:

6=2×3

Example 2: Break down the number 8 into prime factors!

We present the number 8 as a product of 2 and 4! The number 2 is a prime number, but the number 4 is not a prime number, so we continue to break down the number 4 further! The number 4 can be represented as the product of 2 and 2! With this in mind, we can represent the branch of multiples of the number 8, which is represented in the figure below:

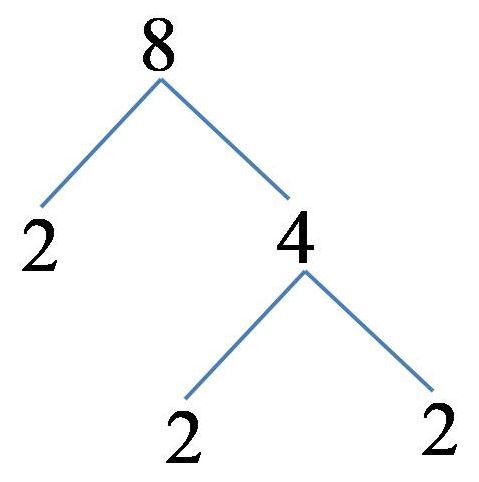
The number 8, through its multiples, can be represented as:

8=2x2x2

Example 3: Break down the number 18 into prime factors!

We present the number 18 as a product of 2 and 9! The number 2 is a prime number, but the number 9 is not a prime number, so we continue to break down the number 9 further! The number 9 can be represented as a product of 3 and 3! With this in mind, we can represent the branch of multiples of the number 18, which is represented in the figure below:

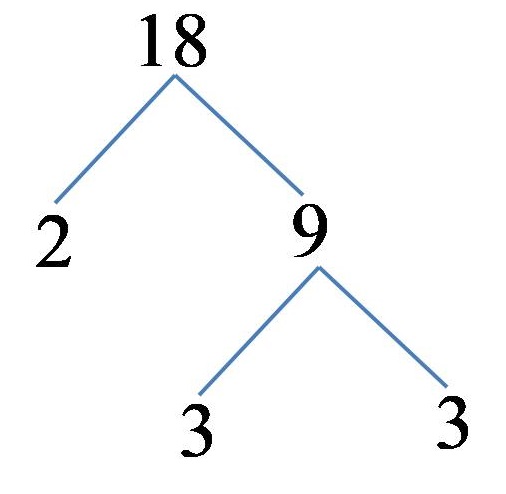
The number 18, through its multiples, can be represented as:

18=2x3x3

Prime Factor Decomposition Table For The Numbers 1 To 100

Below on this page is a table that contains all the prime factor decomposition for all numbers from 1 to 100. Of course, in the table itself, you have data that shows which of the numbers are prime numbers, so logically there is no need to further decompose them!

Number	Prime Factor Decomposition
1	Prime number
2	Prime number
3	Prime number
4	4=2×2
5	Prime number
6	6=2×3
7	Prime number
8	8=2x2x2
9	9=3×3
10	10=2×5
11	Prime number
12	12=2x2x3
13	Prime number
14	14=2×7
15	15=3×5
16	16=2x2x2x2
17	Prime number
18	18=2x3x3
19	Prime number
20	20=2x2x5
21	21=3×7
22	22=2×11
23	Prime number
24	24=2x2x2x3
25	25=5×5
26	26=2×13
27	27=3x3x3
28	28=2x2x7
29	Prime number
30	30=2x3x5
31	Prime number
32	32=2x2x2x2x2
33	33=3×11
34	34=2×17
35	35=5×7
36	36=2x2x3x3
37	Prime number
38	38=2×19
39	39=3×13
40	40=2x2x2x5
41	Prime number
42	42=2x3x7
43	Prime number
44	44=2x2x11
45	45=3x3x5
46	46=2×23
47	Prime number
48	48=2x2x2x2x3
49	49=7×7
50	50=2x5x5
51	51=3×17
52	52=2x2x13
53	Prime number
54	54=2x3x3x3
55	55=5×11
56	56=2x2x2x7
57	57=3×19
58	58=2×29
59	Prime number
60	60=2x2x3x5
61	Prime number
62	62=2×31
63	63=3x3x7
64	64=2x2x2x2x2x2
65	65=5×13
66	66=2x3x11
67	Prime number
68	68=2x2x17
69	69=3×23
70	70=2x5x7
71	Prime number
72	72=2x2x2x3x3
73	Prime number
74	74=2×37
75	75=3x5x5
76	76=2x2x19
77	77=7×11
78	78=2x3x13
79	Prime number
80	80=2x2x2x2x5
81	81=3x3x3x3
82	82=2×41
83	Prime number
84	84=2x2x3x7
85	85=5×17
86	86=2×43
87	87=3×29
88	88=2x2x2x11
89	Prime number
90	90=2x3x3x5
91	91=7×13
92	92=2x2x23
93	93=3×31
94	94=2×47
95	95=5×19
96	96=2x2x2x2x2x3
97	Prime number
98	98=2x7x7
99	99=3x3x11
100	100=2x2x5x5
101	Prime number

Video Examples

We hope that everything that was presented to you above on the page made it easier for you to work with decomposing prime multiples. In the video below, you can see many different examples of prime factor decomposition using multiplier branches!

If you like our method of work and presentation of materials, you are welcome to connect to our pages on social networks, which will allow you to be informed in the future, whenever we publish new content that may be of use to you! All the best!