This post should help you acquire a skill that will bring you success in the procedure of how to simplify fractions before multiplying them! This thinking approach can help you a lot. In the process of multiplication fractions by fractions, the probability of getting an improper fraction is very high. Therefore, if the process of simplifying an improper fraction is problematic for you, you can opt to simplify the fractions before multiplying them, thus removing the need for simplification that usually has to be carried out at the end, with the result you have received in a specific example.
This method can help you in certain instances where it is possible to simplify fractions before multiplying them! This means that this process is not possible in any situation, with any combination of fractions. So pay attention to this guide, to learn to correctly apply the rule mentioned and used below on this page!
How To Simplify Fractions Before Multiplying Them
When practicing simplifying fractions before multiplying them, we should pay attention to the following rules:
- Reduction is possible between the numerator of the first fraction and the denominator of the second fraction
- The reduction is possible between the denominator of the first fraction and the numerator of the second fraction
- Reduction is possible (between the first, second, or both first and second pairs of numbers – mentioned under numbers one and two in this rule) if the numbers of the corresponding pair are divisible by the same number (it is best to divide them by their exact greatest common divisor)!
As can be seen from the rule (ordinal number 3), we can practice simplification with any divisor of the numbers from a corresponding pair of numbers (rule 1 and rule 2), but in this way, we will not simplify the fractions to the simplest possible form. That’s why it’s best to determine their greatest common divisor and simplify with that number!
Examples
Let’s look at relevant examples:
Example 1: Simplify the fractions (if simplification is possible) before multiplying them!
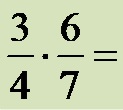
First, let’s look at the numerator of the first fraction (the number 3), and the denominator of the second fraction (the number 7). The numbers 3 and 7 have no common divisor that is different from the number 1, so we cannot simplify this pair of numbers!
Then, we look at the denominator of the first fraction (the number 4), and the numerator of the second fraction (the number 6). We can divide the numbers 4 and 6 by the number 2, which is also the largest of their divisors, so we use that opportunity to simplify the fractions (4:2=2; 6:2=3). The entire procedure for simplifying fractions before multiplying them should look like this:
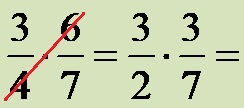
It’s easy!
Example 2: Simplify the fractions (if simplification is possible) before multiplying them!
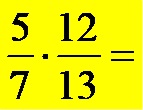
First, let’s look at the numerator of the first fraction (the number 5), and the denominator of the second fraction (the number 13). The numbers 5 and 13 have no common divisor that is different from the number 1, so we cannot simplify this pair of numbers!
Then, let’s look at the denominator of the first fraction (the number 7), and the numerator of the second fraction (the number 12). The numbers 7 and 12 have no common divisor that is different from the number 1, so we cannot simplify this pair of numbers!
As you can see, we can’t simplify the fractions from example number two before multiplying them!
See also the third example given in the continuation of the text.
Simplify Two Pairs
Example 3: Simplify fractions (if possible) before multiplying!
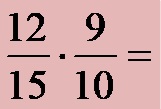
First, we consider the numerator of the first fraction (the number 12) and the denominator of the second fraction (the number 10). We can divide the numbers 12 and 10 by the number 2, which is also the largest of their divisors, so we use that opportunity to simplify the fractions (12:2=6; 10:2=5).
Then, we consider the denominator of the first fraction (the number 15) and the numerator of the second fraction (the number 9). We can divide the numbers 15 and 9 by the number 3, which is also the largest of their divisors, so we use that opportunity to simplify the fractions (15:3=5; 9:3=3). The entire procedure for simplifying fractions before multiplying them should look like this:
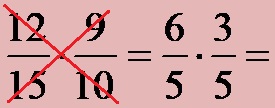
Conclusion
If we decide to analyze the results obtained in the solved examples above in the text, we will come to the following conclusions:
- From the first example, it can be seen that simplification is possible only for a pair of numbers that are placed along a certain imaginary diagonal!
- The second example shows that simplifying fractions before multiplying them is a procedure that is not possible in every case!
- The third example shows that simplifying fractions before multiplication is possible along the two imaginary diagonals, i.e. two pairs of numbers!
Of course, as can be seen in the solved examples above, the procedure is very simple and anyone can practice it without any serious difficulties!
You are welcome if you want to see even more examples of simplification in the video below:
If you liked our site, connect with our social media pages to receive information about our future activities!





