This guide will help you learn how to reduce fractions to the lowest terms. Here we will help you, at the very beginning, to detect whether it is even possible to reduce the fraction or not. Of course, this process of reducing fractions depends on their numerator and denominator. Depending on their size we can complete the process of reducing fractions in a very simple and easy way.
Below on the page you can see solved examples by reducing fractions. The guide contains examples of easier and more difficult levels. Easier level solved examples are here to help you understand the method of reducing fractions in a simple way. The harder level is here to help you see more complicated examples that should form lasting knowledge in each of our readers.
Method Of Learning About Reducing Fractions
In the text below, in addition to the text-based examples, you can also see video examples that are more numerous than the text ones. This kind of presentation of solved examples allows you to see much richer content as well as exercises in more different situations. This type of display also allows you to test yourself – do you know how to reduce fractions to their smallest form. Simply stop the video at a specific moment that you yourself judge you need, and then try to estimate what the outcome will be in the next step of the solution. If you are successful in predictions, it can be said that you have learned well the material presented in the content of this page.
Everyone is welcome to browse all the other content our website has to offer. All contents of this type are with a topic related to mathematical calculations that are simple and every person needs them on a daily basis.
Well, let’s start by considering and solving concrete examples by reducing fractions to their simplest form. Good luck!
Reduce Fractions To The Lowest Terms
When reducing fractions to their simplest form, we first need to see what numbers their numerator (the numerical value above the fractional point) and denominator (the numerical value below the fractional point) are.
First we need to determine if the numerator and denominator are divisible by the same number. If we can divide them by the same number, then that fraction can be reduced. It would be nice if we could determine the largest number by which the numerator and denominator can be divided. Then with a single procedure we will reduce the fractions to their simplest form.
But no worries! It is not wrong at all if we reduce the fraction with a smaller number by which we can divide both the numerator and the denominator, but in this situation we might have to repeat the reduction process several times until we get to the simplest form. Because several ways of solving may appear, below in the text we will see examples of several different approaches to solving. See the first example below:
Examples On How To Reduce Fractions To Lowest Terms
Example 1: Reduce the fraction to its lowest term!
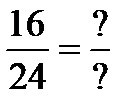
First approach
It is obvious that the fraction from example number one has a numerator of 16 and a denominator of 24. If we observe that the greatest divisor of the numbers 16 and 24 is the number 8, then reducing the fraction looks like this:
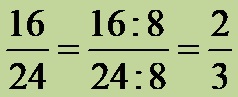
Second approach
If for the same fraction, we decide to divide by the number 4 first, then we get:

However, it is noted that the newly obtained fractional expression can still be reduced. The new numerator 4, and the new denominator 6, are divisible by the number 2. So in this approach, we have an extra step to complete. In the end, after the reduction, we get again the same final fraction in its lowest terms that we already discovered once using the first approach. Look at the solution and make a proper comparison between the different approaches!
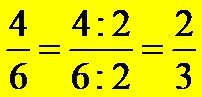
Third approach
If at first, for the calculation, they decided to divide the numerator and the denominator by the number 2, then I get the fraction:
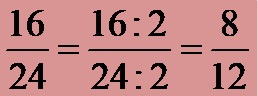
In the newly obtained fraction, the numerator is the number 8, while the denominator is the number 12. Now, we can again divide the newly obtained numerator and denominator by the number 2. If we decide on this step, we get the new version of the fraction:
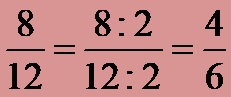
In the new fraction, the numerator is the number 4, while the denominator is the number 6. We can continue the division process. If we divide for the third time by the number 2, we get the same fraction as the final solution, which we already got as a solution in the first and second approaches to solving:
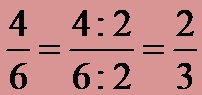
Conclusion
The three different approaches that are presented above on the page clearly show us that no matter how we decide to approach the solution of an example by reducing a fraction we will in any case bring it to a version that represents its simplest form. Of course, the smoothest solution is the solution in which we will divide by the largest divisor of the numerator and the denominator from the very beginning. In that case, the procedure is the shortest. If we decide to divide by a smaller divisor than the largest, then the solving procedure is longer! At least we know that the final solution will always be the same!
Reducing fractions to their simplest form is a process that occurs as a secondary necessity when performing certain mathematical operations. For example, let’s say you need to add or subtract fractions. Then if in the end the sum or the difference can be reduced, you are the ones who should perceive it and automatically, without anyone telling you that there is a need for that procedure, to complete it. The same goes for any other mathematical operation such as multiplying or dividing fractions! So be careful whenever you get a final solution in a particular instance you’re solving, because your final solution might need to be further reduced!
Video Examples Of Reducing A Fraction To Its Lowest Terms
The video below contains many different examples of reducing a fraction to its simplest form. We recommend that you definitely watch the video and learn and determine the procedure for reducing fractions.
If you have any additional questions or comments, you can use the comment form at the bottom of this page! Thank you!





