This guide, to you readers, can help you learn how to divide whole numbers with decimals. Our guide contains everything there is to know, so that everyone can individually adapt and learn the procedure, paying attention to each specific step that you need to complete. Of course, to be able to practice this mathematical calculation without any problem, you should further review our contents that further describe certain mathematical strategies that directly or indirectly correlate with dividing whole numbers with decimals.
Therefore, dear friends, our recommendation to you is to use this guide to the best of your ability. If despite using our guide, you still need help or additional materials, each of you can ask for additional help by commenting in the comment form at the bottom of the page or through the main contact page of this website. But let’s first take a detailed look at the content we offer you here!
Divide Whole Numbers With Decimals
When practicing the mathematical calculation for dividing whole numbers with decimals, we must know that:
- The rules for writing a sign before the quotient (+ or -) apply, the same as when dividing whole numbers!
- At the beginning of the division procedure, we expand the whole number and the decimal number with a decimal unit (10; 100; 1000; 1000), which contains as many zeros as the decimal number has decimal places.
- Finally, during the division process itself, we divide the numbers that we got after the expansion just like any other whole numbers!
If we follow all three rules listed above in the text, we can solve any example by dividing whole numbers with decimals. As you can see, during the procedure we must pay attention to the sign of the quotient, correct expansion, and correct division!
Examples
Let’s look at a concrete example in which we use all three rules. See the first example below:
Example 1: Calculate the quotient obtained when dividing the whole number -66 and the decimal number 1.2!
Before starting the procedure itself, let’s analyze example number one.
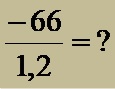
- a) The whole number -66 and the decimal number 1.2 have different signs (the whole number has a – sign and is negative, while 1.2 has a + sign and is positive). Therefore, from the start, it is seen that the quotient will be negative (see rules for dividing whole numbers)!
- b) The decimal number 1,2 has one decimal place, so we expand both the whole number and the decimal number by 10 before dividing them.
- c) We divide the numbers (-660) and (+12), which were obtained after expansion, and get the quotient.
The entire procedure in written form should look like this:
First, we expand both numbers by 10:

We divide the obtained numbers after expansion:
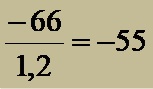
The quotient of the numbers -66 and 1.2 is equal to the quotient of the numbers -660 and 12!
The quotient is -55!
Let’s look at another example of dividing whole numbers with decimals:
Example 2: Calculate the quotient obtained when dividing the whole number -78 and the decimal number -3.25!
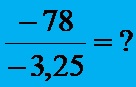
The sign of the result (quotient) is + because when dividing numerous values with the same sign, a positive result is obtained! First, we multiply the numbers from the example by 100, because the decimal number -3.25 has two decimal places.

We divide the resulting numbers after expansion by each other. The procedure looks like this:

The quotient of the numbers -78 and -3.25 is equal to the quotient of the numbers -7800 and -325.
The quotient is 24!
Video Examples
This page below contains a video that has many examples describing how to divide whole numbers with decimals! We offer you the chance to see many more examples that will help you memorize the steps you need to perform every time you want to divide whole numbers with decimals.
If any of you want additional help related to dividing whole numbers with decimals, feel free to ask our team, who are always ready to produce new and specific materials to help all our readers!





