The question is: How do you add 3 fractions with different denominators? This guide of ours aims to facilitate the procedure in which you aim to add more than two fractions that have different denominators. This is probably one of the most important segments of basic mathematics that everyone should know if they have aspirations to become a good mathematician! On the one hand, this is one of the most challenging mathematical procedures, and on the other hand, we have to be a little more careful because we have more parts to collect!
Our new post contains rules that we should respect, as well as examples that show how to apply the rules! On the page below you have solution examples directly on the page itself, while at the very bottom of the page you have a link that leads you to solved examples with the addition of 3 fractions with different denominators in video format that are presented in an even more interesting way compared to those in text form.
Let’s start the learning procedure!
Add 3 Fractions With Different Denominators
When adding 3 or more fractions with different denominators, we should pay attention to the following rules:
- First, we need to determine the LCM (LCD) of all three (or more) different denominators.
- We expand each of the fractions to a form that has the same denominator as the rest. The denominator must equal the LCM of the different denominators.
- In the third step, we easily add the three (or more) fractions, because they have the same denominators.
- Finally (if necessary), if the result is in the form of an improper fraction, we convert it to a mixed fraction!
Examples On Page
Following the above rules, let’s look at some concrete examples:
Example 1: Add the three fractions that have different denominators:
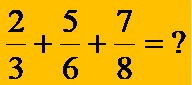
The denominators of the fractions in the example above are the numbers 3, 6, and 8. Our first challenge is to determine the least common denominator of these three numbers (Be sure to read the text that explains how to determine the LCM of two or more numbers if this procedure does not is known to you).
The LCD for the numbers 3,6 and 8 is:
LCD(3;6;8) = 24
In the second step, we expand all three fractions, so that after expansion they all have the same denominator, which is 24. Expanding in this way, we get the expression:
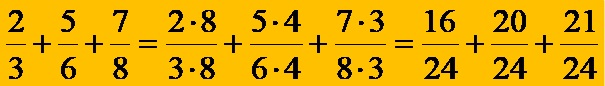
In the third step, we add 3 fractions with the same denominators! Adding the three fractions in this format gives the relation:
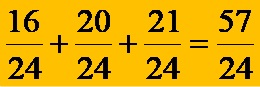
In the last step, we transform the result, which is in the form of an irregular fraction, into a mixed fraction!
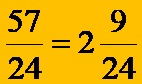
Example 2: Add the three fractions that have different denominators:
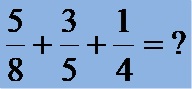
The denominators of the fractions in example number two above are the numbers 8, 5, and 4. We begin by determining the least common denominator of these three numbers.
The LCD for the numbers 8,5 and 4 is:
LCD(8;5;4) = 40
In the second step, we expand all three fractions, so that after expansion they all have the same denominator, which is 40. Expanding in this way, we get the expression:

In the third step, we add 3 fractions with the same denominators! Adding the fractions in this format gives the relation:
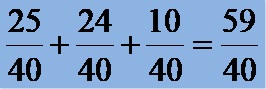
In the last step, we transform the result, which is in the form of an irregular fraction, into a mixed fraction!
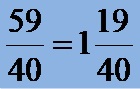
Video Examples
In the video below you can see many examples of adding three fractions with different denominators. We recommend that you take a look at them and use the opportunity to self-test with their help!
Share this page with people who you think need it!




