In today’s text, we will explain everything about the commutative property of addition and multiplication. Because the commutative property applies to both the math operation addition and the math operation multiplication, we decided to cover this unique property in a single post.
Proof Of The Commutative Property Of Addition And Multiplication
This property is one of the most fundamental properties in mathematics. Sometimes we don’t even need mathematics as a subject to learn it. At a certain age, every person has a clear idea of what the commutative property is and why that property applies (is true) to any two numbers that we add or multiply together. All the examples that we see in everyday life indicate the universal truth that describes this property, only sometimes a person does not know what is the name of the rule that describes the phenomenon that he already understood from his everyday life!
For Addition
The commutative property of addition is used when adding two numbers. We can express the commutative property of addition in the following way: The sum (result) we get when adding two numbers does not change if the numbers we add change their places!
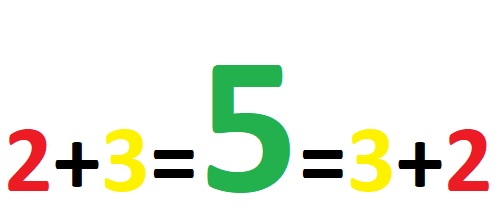
This a very simple rule that is very useful and has great use in further extending math materials! Let’s consider a concrete example that illustrates the commutative property of addition. See the first example below:
Example 1: Prove that the commutative property is true when adding the numbers 7 and 5!
When adding the numbers 7 and 5 according to the arrangement they have in this sentence, it is obtained that:
7+5=12
But on the other hand, if we add the same numbers in reverse order than in the previous sentence, then we get:
5+7=12
With this, we have proved the commutative property of addition, because we have confirmed that the sum of the numbers 7 and 5 (the number 12) does not depend on how we arrange the numbers during the addition! No matter how we add, whether 7+5 or 5+7, the result does not change, that is, it remains the same, equal to 12!
Example For Integers
Let’s now check whether the commutative property of addition is also true for any integers. Therefore in the second example, we will add one positive integer and one negative integer. Look at the second example:
Example 2: Prove that the commutative property is true when adding the numbers -12 and 8!
When adding the numbers -12 and 8 according to the arrangement they have in this sentence, we get that:
(-12)+(8)=4
But on the other hand, if we add the same numbers in reverse order than in the previous sentence, then we get:
(8)+(-12)=4
With this, we have proved the commutative property of addition, because we have confirmed that the sum of the numbers -12 and 8 (the number 4) does not depend on how we arrange the numbers during the addition! No matter how we add, whether (-12)+(8) or (8)+(-12), the result does not change, that is, it remains the same, equal to 4!
Except for natural and whole numbers, the commutative property applies to any type of number you will study in the science of mathematics! Try it yourself, what you get when you try to prove that the commutative property of addition is true when adding two fractions!
Commutative Property Of Multiplication
We can ask the question: Is the commutative property true except for addition and can we extend it to the mathematical operation multiplication? Let’s check that together too!
Suppose that the commutative property for multiplication can be defined as: The product (result) we get when multiplying two numbers does not change if the numbers we multiply change their places!
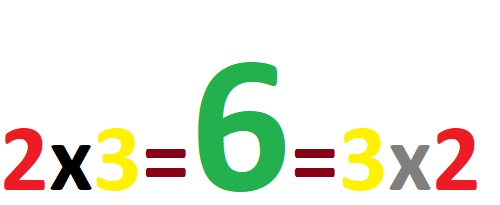
See the third example below:
Example 3: Prove that the commutative property is true when multiplying the numbers 3 and 9!
When multiplying the numbers 3 and 9 according to the arrangement they have in this sentence, we get that:
3×9=27
But on the other hand, if we multiply the same numbers in reverse order than in the previous sentence, then we get:
9×3=27
With this, we have proved the commutative property of multiplication, because we have confirmed that the product of the numbers 3 and 9 (the number 27) does not depend on how we arrange the numbers in the multiplication! No matter how we multiply, whether 3×9 or 9×3, the result does not change, that is, it remains the same, equal to 27!
Through example number 3 we successfully proved that the commutative property of multiplication is true!
Example For Whole Numbers
Let’s check if the commutative property of multiplication is also true for whole numbers. Therefore, in the fourth example, we will consider what happens when we multiply one positive integer and one negative integer if we change the places of the numbers in two different situations!
Look at the following example!
Example 4: Prove that the commutative property is true when multiplying the numbers -2 and 6!
When multiplying the numbers -2 and 6 according to the arrangement they have in this sentence, we get that:
(-2)x(6)= -12
But on the other hand, if we multiply the same numbers in reverse order than in the previous sentence, then we get:
(6)x(-2)= -12
With this, we have proved the commutative property of multiplication for integers as well, because we have confirmed that the product of the numbers -2 and 6 (the number -12) does not depend on how we arrange the numbers in the multiplication! No matter how we multiply, whether (-2)x(6) or (6)x-2), the result does not change, that is, it remains the same, equal to -12!
Like the commutative property of addition, the commutative property of multiplication, except for natural and whole numbers, is true for any other type of number, so we can easily extend it to decimal numbers, fractions, real numbers, etc.
Video Examples
In the video below, you can see examples of proving the commutative property of addition and multiplication in video format. We recommend that you watch the following video:
Every reader is welcome to contribute ideas that include new materials that we will present in the future on our site. If you have any ideas or needs, feel free to send us your facts!





